On pose \(E\) l'ensemble de telles fonctions définies sur une partie de \(\mathcal A\) uniquement.

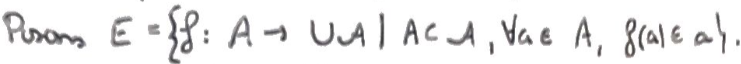
On le munit de l'Ordre partiel associé à la Restriction.

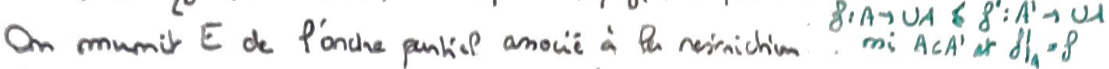
\(E\) est non vide, car il contient la fonction de domaine vide.

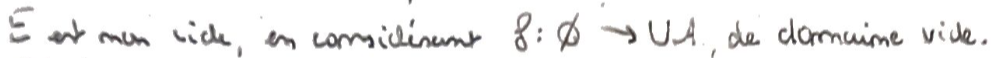
On prend une famille totalement ordonnée et on pose la fonction dont le domaine est l'union des domaines de cette famille \(\to\) \(E\) est inductif.

\(E\) possède donc un Elément maximal d'après le Lemme de Zorn.

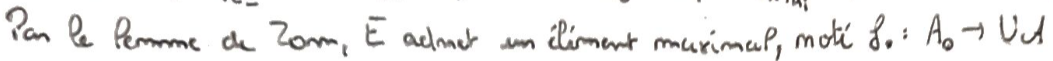
Le domaine de cette fonction est tout \(\mathcal A\), car sinon on peut définir une fonction de plus grand domaine, ce qui contredit sa maximalité.